摩托刹车的距离与汽车比更短吗？

\ Tue Mar 20 2018 00:00:00 GMT+0000 (GMT) \

最近了解到了一个mind blowing的车辆物理的特性，进而发现之前对这个问题的理解一直是有错误的。

刹车距离谁短？

（之前理解的有错，原帖子已经删除）

这家叫做“骑行建议”的网站： http://www.therideadvice.com/can-motorcycle-brake-faster-car/ 。在这篇两年前的文章，尝试了从“物理学”的角度去证明“车重和刹车距离没有关系，只和摩擦力有关”。

其实许多汽车驾驶员也有这样的看法，认为自己的车子有四个轮子，接触面积大，于是刹车上占优势。

如果文章所述是真的，那么这里有两个矛盾的点：

根据文章里头提到的摩擦力公式 f<sub>static</sub> = μ * m * g，轮胎的摩擦力理论上和接触面积没什么关系。但是这其实本身是反常识的，因为日常生活中我们接触到的车辆，为了应付因为载重量增大而带来的刹车问题，通常都会增加轮胎的接触地面积。
另外一个反常识的地方在于，我们都有过这样的体验：同一辆车子，如果载满了人的时候，刹车距离会大大高于空负载的刹车距离。

那么让我们用动能公式的角度来看看这个问题，验证以下是否真是如：

由于机械刹车（除去人为因素）距离的长短，是由动能Kinetic Energy和刹车力Force决定的：

公式： 力 = 动能 / 距离

所以：距离 = 动能 / 力

而动能本身是这样计算的：

动能 = 0.5 * 质量 Mass * 速度 Velocity * 速度 Velocity

因此：距离 = 0.5 * 质量 * 速度^2 / 刹车力

而 摩擦力（即不打滑前提下，可以应用的最大刹车力） = 摩擦系数μ * 重量 并且 重量 = 质量 * 重力加速度

因此：（轮胎摩擦力极限所能提供的）最短不打滑刹车距离 = 质量 * 速度^2 / (轮胎摩擦系数μ * 质量 * 9.8)

推出：（轮胎摩擦力极限所能提供的）最短不打滑刹车距离 = 速度^2 / (轮胎摩擦系数μ * 9.8)

咦！？质量确实在等式中被约掉了。究其原因，是因为质量的增加虽然增加了动能，但同时增加了轮胎的静摩擦力。考虑到现代车的刹车系统都足够锁死轮胎，因此，有理由相信轮胎的摩擦力极限是能够轻松达到的。

然而我们的高中物理和上面文章里头，对于摩擦系数μ的理解不够全面。

高中的书本里通常针对不同的材料，提供了一个固定的静摩擦系数。然而现实中，许多材料的摩擦系数，随着负载增大，其实是会降低的。比如铝：

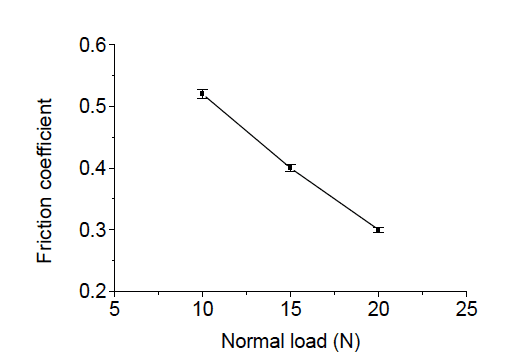
铝的摩擦系数，随着压力改变而减弱

轮胎也是这样，随着载重质量的增大，摩擦系数减小。因此上面的计算中，因为增加重量所增长的摩擦力，并没有预计中那么大，无法完全中和质量增长带来的动能。

因此，质量增加仍然会有效的增加刹车距离。

出于同样的原因，重负载的车子也更容易锁死轮胎。所以增加轮胎面积来减少单位面积内轮胎的压力，从而让摩擦系数的降低不那么影响刹车，也就是理所当然的方案了。

References: